Betz Limit Of Wind Turbines
The Betz Limit Defines Wind Turbine Efficiency
![]() The Betz Limit is a key concept in the design and operation of wind turbines as it helps us understand the maximum energy extraction possible from the wind onto the rotor blades by setting a theoretical upper limit on the efficiency of any wind turbine, regardless of design.
The Betz Limit is a key concept in the design and operation of wind turbines as it helps us understand the maximum energy extraction possible from the wind onto the rotor blades by setting a theoretical upper limit on the efficiency of any wind turbine, regardless of design.
Among the various renewable energy sources, the wind provides an environmentally friendly but intermittent source of renewable energy. Wind turbine generators (WTG’s) of different sizes and designs are successfully used to convert the kinetic energy of the wind into both mechanical and electrical energy. The Betz Limit for wind turbines along with his associated law’s allows us to understand the maximum power that can be extracted from the oncoming wind as it passes through the turbines blades.
We may think that the bigger and more efficient these wind turbine generators are, the more energy they will produce. But this is not the case, as there is a maximum limit to the efficiency of any wind turbine generator in converting the energy of the wind into usable energy. This limit is defined by the Betz Limit of wind turbines.
What Is Meant By The Betz Limit
The Betz Limit, or Betz Law, calculated by German physicist Albert Betz nearly a century ago, states that no wind turbine generator can convert more than about 60% of the kinetic energy of the wind into mechanical (or electrical) energy simply be turning the blades of a rotor.

Since wind moves erratically around from place to place carrying with it kinetic energy, wind direction and wind velocity are therefore subject to both rapid and frequent changes. So any wind turbine must be designed to respond to both conditions as it rotates about a central axis.
Generally, a wind turbine generator (WTG) generates power (P) proportional to the volumetric flow of the wind through it. This results in a pressure difference between the wind entering the rotor blades swept area and leaving it as energy is extracted as it does so.
Thus the overall efficiency of a wind turbine is measured by how effectively the turbine can convert the energy within the wind into mechanical or electrical power.
A Wind Turbines Coefficient of Power
The Coefficient of Power (CP) allows us to calculate the total amount of power a wind turbine is producing from the total energy available in the wind at a particular wind speed. For example:
Coefficient of Power, CP
| CP = | Energy produced by the wind turbine |
| Total Energy available in the wind |
Clearly there are basic physical processes that limit a wind turbines maximum rotor power with the efficiency of a wind turbine at a particular site or location. Thus the energy extracted will depend on various factors, such as:
- The velocity of the oncoming wind, which is constantly changing.
- The rotational speed of the wind turbine blades.
- The type and design of wind turbine.
- The length and swept diameter of the blades.
So the conversion power of a wind turbine is related to design and is defined as the ratio of the net power output to the wind energy input. But the actual power available to rotate the turbine blades is only a fraction of the total theoretical power available in the wind as friction, drag and the swirling action of the air around the wind turbine rotor blades all contribute in reducing efficiency. Therefore, not all the wind’s energy is converted into usable mechanical (or electrical) energy due to these additional losses.
We know that wind turbines convert the winds energy into mechanical or electrical energy as a direct result of slowing down the oncoming wind as it transfers part of its linear kinetic energy to the rotor blades.
But a turbines rotor blades captures only part of the available oncoming wind energy passing through the swept area of the rotor blades. For a wind turbine to be 100% efficient, it would have to stop 100% of the available wind which is clearly not possible, as the rotor blades would have to rotate as one solid disk.
Clearly, if the turbines rotor was constructed as one solid disk design it could not pass any wind energy at all, so it would not be rotated by the wind and therefore no kinetic energy would be extracted or converted.
If we go to the other extreme where a wind turbine had just one single thin rotor blade. Possibly 90% or more of the oncoming wind energy would pass directly through the rotational (swept) area of the single turbine blade missing it completely. Therefore, very little of the winds linear kinetic energy would be converted using a turbine generator with just one single rotor blade.
So there has to be some middle ground in which the number of rotor blades, the volume of air passing through the swept area, as well as the limitations and vortex effect behind the rotor blades produces the ideal or theoretical maximum efficiency from a available wind.
Wind Power Calculations
It is commonly known that the theoretical wind power per given swept area by a wind turbine is generally given by the equation:
Where: P is the power in watts, ρ (rho) is the air density in Kg/m3, A is the circular area (πr2 or πd2/4) in m2 swept by the rotor blades, V is the oncoming wind velocity in m/s, and CP is the power coefficient (efficiency) which is the percentage of power in the wind that is converted into usable energy.
Thus, the wind power output is directly proportional to the cubic power of the wind velocity and to the square of the diameter of the wind turbine. Which is interesting to note, because, when the wind velocity is doubled, the power output is increased by a factor of eight.
Equally as mentioned above, it is not possible to extract all the energy from the oncoming air which passes through the swept area of the rotor blades. As to do so would mean that the air would stop and pile up behind the rotor blades preventing any additional air flow through the blades, irrespective of the specific wind turbine used.
So German physicist Albert Betz carried out some experiments and concluded that no wind turbine could convert more than 59.3% (approximately 16/27) of the kinetic energy contained in the oncoming wind can be converted into usable power simply by turning rotor blades. So how did he come up with this 59.3% maximum value to produce what is now taken as being the Betz limit.
The Betz Limit Equation
If we assume that the direction of wind velocity through the rotor blades is centric, uniform and of a constant velocity over the entire rotor area, the turbines efficiency would be the ratio between the output power, POUT, and the wind energy available flowing into the blades, PIN. Based on these two values, the efficiency of the turbine is thereby given as: η = POUT/PIN.
Thus for a standard wind turbine to be 100% efficient, η must be equal to “1” (η = 1). However, due to the effect of design, friction and windage, the maximum efficiency that could be extracted is actually given as a percentage of the Betz limit. Consider the following wind turbine image showing how the air flows through it.
Wind Turbine Air Flow
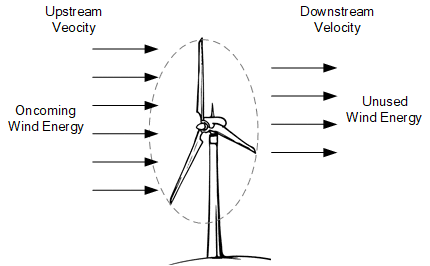
The airflow through the rotor blades consists of two parts. The oncoming wind before passing through the rotor blades, and the outgoing unused wind expelled or retarded by the rotor blades. If the oncoming wind speed (before the rotor) is defined as VIN and outgoing wind speed (after the rotor) is defined as VOUT, then the reduction in airflow would be given as: VOUT - VIN.
Clearly then, the maximum extraction of kinetic energy from the wind is achieved when the largest wind slowdown is produced but still maintaining sufficient air speed (velocity) past the turbines blades. From his observations and calculations, Betz found that no more than about 59.3% of the kinetic energy can be extracted from the incoming (VIN) wind using an optimal three bladed design.
Then we can modify the above equation for the “theoretical” power output from a wind turbine as being:
Where: CP has been replaced with the Betz Limit of 59.3% (0.593) that corresponds to the maximum of the power coefficient. However, this assumes that the power extraction of the turbine generator is without any loss at 100% efficiency. In reality, turbines with 100% efficiency is not possible even when rotating at full speed due to the mechanical nature of their design and operation.
Modern wind turbines operate at between 60 and 80% efficiency depending on type and manufacturer. So if we assume our brand new wind turbine generator is declared as being 80% efficient by the manufacturer, then it will convert 80% of the Betz Limit into electricity. Therefore, the CP of our wind turbine would be: 0.8 x 0.593 = 0.474 (or 47.4%). In other words our wind turbine would convert only 47.4% of the available wind energy into usable electricity and NOT 80%.
Betz Limit Worked Example
The specifications given by a manufacturer of its 3.5kW horizontal-axis wind turbine generator, states that it will operate at its peak efficiency when rotated by a wind velocity of 12 meters/second. At this wind speed it reaches 69% efficiency. What will be its overall coefficient of power taking into account the Betz limit.
That is 41% at a wind velocity of 12 m/sec.
Betz Limit Tutorial Summary
We have seen here that wind turbines are designed to extract as much of the kinetic energy contained within the movement of the air as it passes through its blades. The efficiency of wind power extraction is determined by the Power Coefficient (Cp) which is the ratio of power extracted by the turbine to the total power available in the wind.
As discussed, 100% extraction of the winds kinetic energy is not possible as the flow of the air would be reduced to a complete stop leaving no wind speed available to sustain the flow of air through the wind turbines blade design. German physicist Albert Betz calculated that any wind turbine could not convert more than 59.3% of the kinetic energy available in the wind into mechanical energy simply by turning a rotor blade.
Thus, the maximum coefficient of power is known as the Betz Limit, or the Betz criteria of wind energy which sets the theoretical upper limit on the efficiency of any wind turbine, regardless of design.
There are many factors that prevent real wind turbines from reaching the theoretical Betz limit such as blade losses, mechanical losses, friction, aerofoil drag loss, and many more. In reality actual wind turbines typically achieve about 35-45% efficiency, so reducing these losses will help increase the overall efficiency of a practical wind turbine.
Note that the use of a verical axis wind turbine is not limited by the Betz limit since it can receive the driving force of the wind from all directions around itself.
learn More About The Betz Limit For Wind Turbines
To get a better understanding of how the Betz limit relates to the power produced by wind turbine generators, or to obtain more wind energy information about the various wind turbine generating systems available.
Then order your copy today of the excellent book: Wind Power For Dummies that explores the advantages and disadvantages of wind power and how you could use it to power your home.











This is a really nice post, it explains these principles very clearly, thank you.
I do have one question…
I didn’t quite understand the sentence “Note that the use of a verical axis wind turbine is not limited by the Betz limit since it can receive the driving force of the wind from all directions around itself”.
It seems (to me) that no matter which direction the wind comes from, a VAWT turbine still has to let some of the air-flow pass through it, or it will stop incoming wind, just like a HAWT.
The number may not be 16/27 (~0.593), but the principle still holds true, right?
If it’s not Betz’s limit, what is the theoretical limit for VAWTs?
I’d appreciate any help with this matter.
Thank you.
Unlike the standard horizontal-axis wind turbines (HAWTs) which uses 3-blades that sweep in a clearly defined circular pattern perpendicular to the wind direction in order to extract the winds energy, vertical-axis wind turbines (VAWTs), such as the Darrieus and Savonius designs, have a more complex interaction with the wind limiting their performance and overall efficiency.
As their rotor blades rotate around a fixed vertical axis, they experience a constantly changing angle of attack as they move into and out of the winds flow creating turbulance around themselves. Aerodynamicaly designed VAWTs, could theoretically produce higher amounts of energy extraction than specified by the Betz limit under certain windy conditions, but most commercially available VAWTs operate at a much lower efficiency level of around 50% or less in the real-world.
I don’t quite get the determination of the “Betz Limit”, (59.3%, a very specific number). From the article, he calculated it from his observations. And, for “optimal three bladed design”. What the heck is that?
If one where to go the other way, and think about using electricity to generate wind (an electric fan), I have never seen a fan with three skinny blades.
As stated in the tutorial, a wind turbine, even an ideal one can not convert more than 60% of the available power in the winds kinetic energy to electric power. Betz law calculates the theoretical maximum flow of energy that can be derived from flowing air using a three-bladed rotor at a certain speed as shown in the tutorial. Generally, vertical axis wind turbines have a conversion efficiency of between 25% to 45% due to several mechanical factors.
Wind turbine generators use three-blades as it provides a smoother rotation with less drag compared to one, or two-bladed designs. Also, three-blades offer a better power output, stability, and cost-effectiveness as well as reduced rotational noise levels compared to other rotor designs.
As for your analogy of a fan, it is not valid since electric fans consume electric power to rotate at high speeds to project moving air over a long distance. Appropriately sized and shaped blades contribute to improved air circulation at high speed. Most low speed ceiling fans are three-bladed designs.
Huh. I have three ceiling fans. Two are four bladed and one is five bladed.
I am not good at physics (especially Quantum Physics); but, I get conservation of energy. And, one will never get a turbine to extract the momentum from moving air such that the air will not be moving beyond the turbine blades.
The Betz limit might well be right. It’s a theory derived mathematically* (not experimentally), from conservation of energy equations, and with assumptions.
Now, consider a large duct. Inside the duct is a multiple of highly efficient turbine generators. Let’s say each can extract 50% (less than the Betz limit) of the energy from the wind in front of it. Then, the next generator get’s 50% of the reduced wind. Etc.. The next thing you know, the whole duct system exceeded the Betz limit! :-).
Being the Devil’s Advocate, I’m guessing that your article used Ai (Artificial intelligence).
* I found theoretical derivation of 59.3% in Wikipedia.
Again, none of your comments are valid. A series of turbine generators will not exceed the Betz limit, its just nonsense. You are quoting Wikipedia, so you argument is flawed, and no, we do not use “Ai”, just experience of working in the industry. Goodbye.
Very good article. I learned a lot about wind turbines.
After thinking about it, my guess is that wind turbine generators generally have only three thin blades is because they (the blades) are sufficient to turn the generator and produce all the energy its magnets can generate. Catching more wind or turning faster could not produce more electrical energy.
The blades are expensive, difficult to transport and install, and do not last forever.
Thanks again for the information. Goodbye
I wish I could just copy or download this article
I don’t know how to save it for future sharing or use.
Great article – should be compulsory reading for anyone contemplating buying a wind turbine generator. How do we hold Amazon, AliExpress, eBay etc accountable for the ridiculous performance claims made for the turbines they sell?
Thank you great and simple info
The development of VAWT has been hampered by their low efficiency.
Their construction generates large-scale vortices, generating massive flow separation.
These severe load fluctuations jeopardize the turbine’s structural integrity.
Sandia National Laboratories in Livermore, California, is actively researching and developing vertical-axis wind turbines (VAWTs) for offshore applications, particularly focusing on floating platforms. Their work, including the ARCUS project, aims to reduce the cost of offshore wind energy by optimizing VAWT designs and integrating them with floating platforms. Here’s a more detailed look at their efforts:
ARCUS Project:
This project focuses on designing a towerless VAWT system that minimizes mass and cost, especially crucial for floating offshore wind turbines.
Cost Reduction:
Sandia’s research aims to reduce the overall cost of energy (COE) by optimizing VAWT designs and integrating them with floating platforms, potentially achieving a 20% reduction in COE compared to traditional horizontal-axis wind turbines (HAWTs).
Floating Platform Integration:
The VAWT design allows for a lower center of gravity and easier access to the drivetrain, reducing the size and cost of the floating platform needed to support the turbine.
Advanced Modeling:
Sandia has developed a design tool that simulates the complex interactions between the VAWT, the floating platform, and environmental conditions (wind, waves, etc.).
Commercialization:
Sandia is working on developing manufacturing techniques, certification methods, and commercialization plans to accelerate the deployment of VAWT technology.
Comparison to HAWTs:
VAWTs offer several advantages over traditional HAWTs for offshore applications, including the potential for lower platform costs, easier maintenance, and the ability to be placed closer to the water.
Specific Design Features:
Sandia’s ARCUS design replaces the traditional tower with lighter, tensioned guy wires and utilizes a structurally efficient design that allows for rotor area control in high winds.
Patented Technology:
Sandia has patented a “towerless” VAWT design (U.S. Patent 11,421,650 B2) that addresses the high costs of floating offshore wind.
Sandia’s research on VAWTs for offshore wind is part of a broader effort to advance climate security through science and technology.
This article explain the basics of wind energy and wind turbines and its specific characteristics such as power coefficient. I would like to know how power coefficient is enhanced (not up to Betz limit) for a VAWT. What factors must I consider for high power coefficient (e.g. how much wind velocity, tip speed ratio, etc.)?