Measuring the Power of a Solar Panel
How To Measure the Output Power of a Solar Panel
When measuring the power of a solar panel the use of a digital multimeter is required to measure the voltage and amperes being generated by a panel under different light conditions. Knowing the power output of a particular photovoltaic panel is an important requirement of any solar system.
As we have seen throughout this website, solar power is a renewable form of electrical energy generation that is commonly created using photovoltaic solar panels, either individually or connected together in strings to form larger solar array’s.
Understanding the way that photovoltaic (PV) solar panels work is a basic requirement as most people assume, rightly or wrongly, that just because they have purchased a 100 watt solar panel, it will deliver 100 watts of electrical power continuously all day. However, in reality this is not always the case as the electrical power delivered at a certain instant in time during the day is a direct function of positioning and the weather conditions.
Sunlight is an intermittent energy source constantly changing throughout the day so photovoltaic solar panels have to be able to operate under these varying conditions. As the efficiency of a solar panel is the ratio of electrical power output to the amount of sunlight, that is solar irradiance absorbed by the panel.
Therefore it is important that the solar panel orientation is correct to receive the maximum amount of sunlight throughout the day. Larger panels have the capability to produce more electrical power than smaller PV panels for a given solar irradiance.
The performance of photovoltaic solar panels can be determined by measuring the relationship between the panels voltage, current, and therefore power output under different meteorological conditions, such as total solar irradiance.
Inclination of the panel, ambient air temperature as well as panel temperature all play an important role in the output power of a solar panel.
Manufacturers rate their photovoltaic panels based on the DC output power at an irradiance of 1000 W/m2 (full sun) and a panel temperature of 25oC in order to get you to buy their product.
A standard 12-volt PV panel will generate a maximum terminal voltage of about 20 volts in full sunlight with no connected load. However in the real world, photovoltaic solar panels operate below these ideal settings resulting in the output power of a solar panel being much less than the PV panels possible maximum output power rating.
So how do we measure the output power of a photovoltaic solar panel. Well in its most basic of terms, the output power (P) of the solar cell is obtained by multiplying the output voltage (V) by the output current (I) at maximum power conditions, giving P = V x I which itself is the basis of Ohm’s Law
Solar Panel Power Output
The output power of a typical solar panel depends very much on the electrical load connected to it. Maximum power is transferred when the panel’s (or array’s) dynamic resistance equals that of the connected load. The simplest load for a pv panel to supply current too is that of an electrical resistance such as a DC water heating element. As Ohm’s Law describes the relationship between the voltage across and the current flowing through a resistor, we can use a simple resistance to measure the power of a solar panel.
Solar panel I-V Characteristic Curves are used to give a visual representation of the current and voltage ( I-V ) characteristics of a particular photovoltaic panel (cell or array) giving a detailed description of its solar energy conversion ability. Knowing the electrical I-V characteristics of a solar panel is critical in determining the output performance and therefore its efficiency. Measuring the output power of a solar panel, for example the 100W, 12V Renogy Solar Panel is not that difficult if we apply some simple steps.
The product label of the Renogy 100 Watt 12 Volt Polycrystalline Solar Panel gives us the electrical characteristics of the panel, according to the manufacture Renogy when it is exposed to an irradiance of 1000 W/m2. But what does it all mean.
Our electrical data label states that the panels Open Circuit Voltage, (VOC) is 22.4 volts and that its Short Circuit Current, (ISC) is 5.92 amps.
So we can use Ohm’s Law then to find the output power of the solar panel, right!. But V times I gives us 22.4 x 5.92 = 132.6 watts, which is a lot more than the 100 watts quoted by Renogy, so what’s going on?
The open-circuited voltage, VOC means that the PV panel is not connected to any load, so its terminals are therefore open (infinite resistance) resulting in maximum voltage, in this case 22.4 volts, at its terminals. As its terminals are open there will be no current flow (I = 0) because there is no electrical circuit or load for the current to circulate through. Then the output power of the solar panel in this instance is P = V x I = 22.4 x 0 = 0 watts. In other words no generated electrical power.
Likewise, the short-circuited current, ISC means that the PV panels terminals are shorted or connected together (zero resistance) creating a fully closed electrical circuit allowing maximum panel current, in this case 5.92 amps, to flow. However, as the terminals are shorted together there will be no output voltage drop (V = 0), so the output power of the solar panel will be P = V x I = 0 x 5.92 = 0 watts. Again no generated electrical power.
Then we may think that this Renogy solar panel can generate 132.6 watts of solar electricity, in reality it can not. Photovoltaic panels provide usable electricity when connected to an electric load and by measuring the output of a solar panel, we can use Ohm’s Law to determine the maximum output power point, or MPP.
Measuring the Power of a Solar Panel
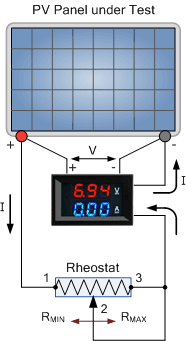
We said previously that the output power of a solar panel mainly depends on the electrical load connected to it. This load can vary from an infinite resistance, (∞Ω) to a zero resistance, (0Ω) value thus producing an open-circuit voltage, VOC at one end and a short-circuit current, ISC respectively, at the other. Then we need to be able to find an external resistive value somewhere inbetween these two extremes.
As the theoretical maximum power, Pmax was shown to be 132 watts, and the maximum open-circuit voltage, VOC as 22.4 volts. If we assumed the panel has a maximum wattage of 150 watts and a maximum terminal voltage of 30 volts, this would give us the panels dynamic resistive value of:
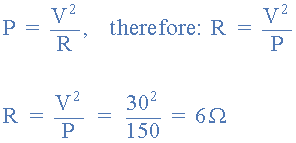
There are many ways to achieve this 6.0 Ohm value using fixed value resistors, to variable resistors, to rheostats. The option used would depend on what’s available and budget, as large power resistors can be expensive. In the example given, the load resistance will be achieved using a Rheostat, thus giving us a fully variable resistance between a minimum value of zero Ohms (0Ω) and the maximum value of 6Ω. We know that our solar panel has a manufacturers rating of 100 watts, so this would be the minimum power rating of our rheostat.
To measure the voltage across the terminals of the PV panel we would require a voltmeter. This could be a digital or analogue multimeter or a simple voltmeter but must have a scale high enough to read the panels open-circuit voltage (VOC). The type used would depend on what’s available and budget.
Measuring the current generated by the PV panel would require an ammeter to measure the short circuit current (ISC) into a dead short. Again this second meter could be digital, analogue or a multimeter depending on what’s available and budget.
Although we have calculated the maximum resistive value required above as being 6Ω, chances are we would not be able to purchase one at the exact 6Ω resistive value. So let’s assume that we bought a 10Ω rheostat which is fully variable from between 0 and 10 Ohms.
This would allow us to increase the externally connected load resistance in 10 steps of 1 Ohm each, while at the same time measuring the solar panels output voltage and current. Then we can complete the following table of our results to determine the electrical power supplied by the PV solar panel for different values of load resistance.
Table of Measured Results for our Solar Panel
| Resistance (in Ohms) | Voltage (in Volts) | Current (in Amperes) | Power (in Watts) |
|---|---|---|---|
| Open Circuited | 22.4 | 0.00 | 0.00 |
| 10 | 22.4 | 2.24 | 50.2 |
| 9 | 22.3 | 2.47 | 55.1 |
| 8 | 22.1 | 2.76 | 61.0 |
| 7 | 21.6 | 3.08 | 65.9 |
| 6 | 20.80 | 3.50 | 72.8 |
| 5 | 20.05 | 4.01 | 80.4 |
| 4 | 18.80 | 4.70 | 88.4 |
| 3 | 16.86 | 5.62 | 94.7 |
| 2 | 11.60 | 5.80 | 67.3 |
| 1 | 6.0 | 6.00 | 36.0 |
| Short Circuited | 0 | 5.92 | 0.00 |
Having taken our readings and tabulated the results in the above table, we can clearly see that the maximum power occurs when the load resistance RL has a resistive value around the around the 3 Ohms value. At 3Ω’s the panel produces a current of 5.6 Amperes at about 16.9 volts, thus giving a calculated output power of 94.7 watts.
This value closely matches the manufactures data label for an operating voltage (Vmp) and operating current (Imp) of 17.8V and 5.62A respectively giving a dynamic panel resistance at maximum power of Vmp/Imp = 17.8/5.62 = 3.17 ohms. We could if so wished fine tune our measurements to get voltage and current values even closer to the 100 watt, 3.17 ohms target.
It therefore shows for our simple example that the maximum power is generated by the panel around this 3.17 ohms point and matching panel resistance to load resistance results in maximum power transfer from panel (or array) to load and therefore, increased efficiency.
Using the data from the table above, we can plot a graph of the measured voltage against the panels current as shown.
I-V Characteristics Curves
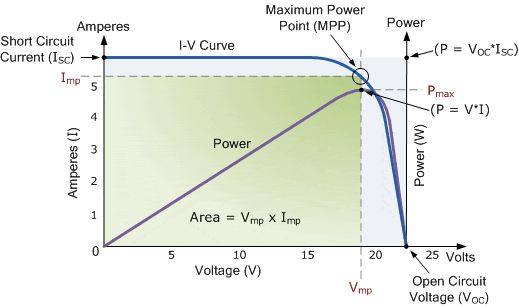
Above is the I-V characteristics graph for our PV solar panel example and is typical for all PV solar panels. Measuring the power of other types and ratings of solar panel will produce similar results, just the voltages and current values will be different. Also notice that power is zero for an open-circuit (zero current condition) and also for a short-circuit (zero voltage condition).
The maximum power output of a PV panel can be defined as its peak DC output given by multiplying the voltage and the current. Here the optimum operating point for our solar panel is shown at the mid-point in the bend (or knee) of the characteristics curve. In other words, this is the point at which the solar panel generates its maximum power, known commonly as the maximum power point or MPP.
The I-V characteristics curve presents an important property of a photovoltaic solar panel, or cell in that it shows it to be a current source device rather than a voltage source device, like a battery. However, unlike a battery which has a constant terminal voltage, (12V, 24V, etc.) and provides variable amounts of current to a connected load, the photovoltaic cell or panel provides a constant supply of current over a wide range of voltages for a given amount of solar insolation.
Measuring the Power of a Solar Panel Summary
Measuring the power of a solar panel is not too dificult but requires an assortment of multimeters, power resistors, or a single rheostat capable of handling the generated power. We need to remember that the greater the power output of your panel. For example, 200W, 285W, 330W, etc. the greater will be the voltages and currents and therefore safety is important.
